Overall Process
For a simulation, you will experience following 6 steps:
1.Data Input
2.Configure simulation parameters
3.Add portfolio-optimization algorithms
4.Configure estimation methods, parameters and constraints for each algorithm
5.Configure diversification method and corresponding parameters
6.Run simulations and view outputs
Please Note：If you select multiple parameters for Simulation and Algorithms, we will provide you with a combination of all these parameters. For example, if you select 3 parameters for Simulation and 2 Portfolio-optimization Algorithms, we will provide you with a group of 6(3×2) models. You can choose to run any one or more of them.
1. Data Input
You can either upload your own data or load from our database.
To upload your own data, check if the data format is valid:
- The filename extension should be (.csv) or (.txt) with <,> as separator.
- The first row should be names of assets.
- The first column should be a date sequence.
- Each cell represents the price of an asset at a certain date.
For instance, the sample data looks like below:
To upload your own data, you may:
1.Select “Upload own data”;
2.Choose a file then click “Upload CSV File”;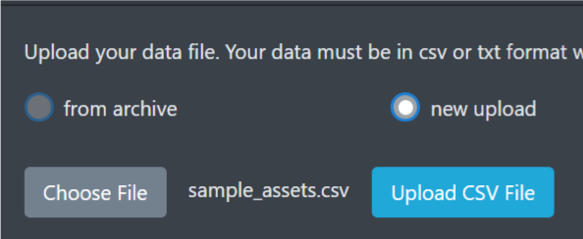
We temporarily save uploaded data files at archive.
Before next login, you don’t need to upload your data again.
Tick “from archive” and choose the file you have uploaded.
3.Configure simulation dates interval after uploading data.
(Note that: periodical rebalances begin from the first day of the interval.)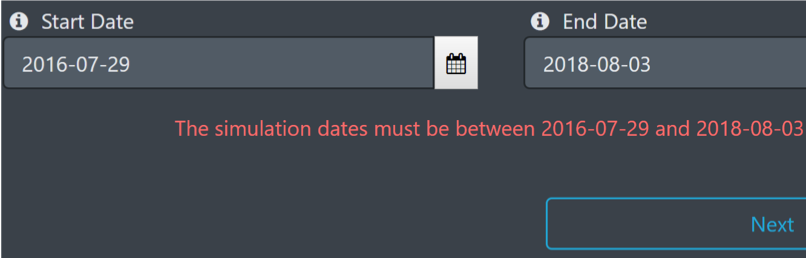
4. Click “Next”.
2. Simulation Parameters
Next, you need to configure two important simulation parameters:
Data Window Size
Usually, rebalancing requires estimation of expectation and covariance of returns using historical data within a given period whose length is data window size. For example, If we set the window size to 6 months, when rebalancing on 1st July, 2010, the calculation will base merely on the data within 6 months(1st Jan. 2010 ~ 30th Jun. 2010).
Rebalancing Period
This parameter is denoted by the interval between two adjacent rebalances.
You can configure more than 1 parameter sets.
Note that sometimes you may receive a warning like this:
This is because the data which will be used to do mean and covariance estimations for the first rebalancing are insufficient according to the window size. We need mean and covariance estimations based on the data in the window to rebalance.
If the data in the window are not enough, some errors will occur.
For example, if your file includes data from 2010-01-01 to 2019-01-01, your simulation start date is 2011-01-01 and data window size is 2 years, then the first rebalance will be based on 2009-01-01 to 2011-01-01. You don’t have the data from 2009-01-01 to 2009-12-31.
Possible solutions are:
1.Provide larger data file that includes earlier data;
2.Postpone your simulation start date;
3.Configure smaller data window size.
For example: if your source data starts on 2016-07-29 with a simulation start date 2016-10-29 and a 6 months data window size, methods to eliminate the warning for you will be:
1.Provide a data file that includes data beginning from 2016-04-29;
2.Set your simulation start date as 2017-01-29;
3.Set smaller data window size like 3 months or 1 month.
3. Portfolio-optimization Algorithms
Now you need to configure the portfolio-optimization algorithms for test.
We provide 4 kinds of algorithms: 1/N, Markowitz, SOCP and SAAM, where Markowitz, SOCP and SAAM are all based on modern portfolio theory.
1/N Algorithm
1/N represents equal weighting algorithm. At each rebalance, the whole money will be evenly distributed among all assets.
This algorithm is often used for comparison with other portfolio-optimization algorithms.
Markowitz Algorithm
Markowitz algorithm tries to balance benefits with risk based on investor’s risk aversion level. It solves
\(\max_{w} w^{T}r-\lambda w^{T} \Sigma w\) s.t. \(\ w^{T}1=1\)
SOCP Algorithm
Different from Markowitz’s quadratic programming solution, SOCP (second-order cone programming) is a convex optimization problem of the form
\(\min f^T x\)
subject to \(||{A_i x+b_i}||_2\) ≤ \(c_i^Tx+d_i\), i=1,2,…,m
\(F_x=g\)
where the problem parameters are f∈\(R^n\), \(A_i∈R^{d n_i*n}\), \(b_i∈R^{n_i}\), \(c_i∈R^n\), \(F∈R^{p*n}\), \(g∈R^p\).
\(x∈R^n\) is the optimization variable.
WHY SOCP?
When adding some complicated constraints into Markowitz model, the newly formed optimization problem may not belong to quadratic programming problems, so we introduce the more general programming method SOCP to solve the new problem. Solving a SOCP problem is also more time-efficient than solving the traditional quadratic programming problem even for original Markowitz model.
SAAM Algorithm
SAAM [1] (stochastic asset allocation method) develops Markowitz’s algorithm by considering future returns and risks as random variables. It solves
\(\max \limits_{η}\) {\(E[w^T(η)r_{n+1}]\)-\(\lambda Var[w^T(η)r_{n+1}]\)}
w(η)=arg \(\min \limits_{η}\) \(\lambda E[{w^Tr_{n+1}}^2]\)-\(ηE(w^Tr_{n+1})\)
SAAM also uses bootstrapping methods for resampling, which attenuates the bias of estimated effective weight vector.
More information about SAAM Algorithm can be seen here.
4. Algorithm Parameters
Parameters for each algorithm are as below:
For Markowitz and SOCP algorithms, we provide 3 methods to estimate returns.
Returns Estimation Models
―Sample Mean:
Use mean of the sample data within the estimation window as returns.
\(r_i=\frac {\Sigma^m_{j=1}r_{ij}} {m}\)
―Equal Mean:
Assume each asset shares the same expectation of return. Calculate average returns of all assets as each asset’s expectation of return.
\(\bar r\)=\(\frac {\Sigma^n_{i=1}r_i}{n}\)
―Linear Shrinkage:
Based on Sample Mean but shrink to Equal Mean. The estimated expectation of return is calculated as below:
\(r_i^{′}\)=\((1-\sigma)r_i+\sigma\bar r\)
For SOCP and Markowitz algorithms, we provide 4 methods to estimate covariance matrix.
Covariance Matrix Estimation Models
―Sample Covariance:
Use covariance of the sample data within the estimation window for estimation.
\(\Sigma=(\Sigma_{ij})\)
\(\Sigma_{ij}=\frac{1}{m-1}\Sigma_{k-1}^m (r_{ik}-r_i)(r_{jk}-r_j)\)
―Equal correlation:
Assume every two different assets shares the same correlation, which is
\begin{equation}
\label{eq6}
\rho_{ij}=\left\{
\begin{aligned}
1, i=j; \\
c, i\ne j.
\end{aligned}
\right.
\end{equation}
where c is a constant.
Use maximum likelihood estimation to calculate this correlation and then the covariance matrix:
\(\Sigma_{ij}=Cov(X_i,X_j)=\rho_{ij}\sigma_i\sigma_j\)
―Linear Shrinkage:
Based on Sample Covariance but shrink to Equal Correlation. The estimated expectation of covariance matrix is calculated as below:
\(\Sigma^{′}=(1-\delta)\Sigma+\delta F\)
where F is the covariance matrix calculated by equal correlation method.
―Nonlinear Shrinkage:
The best known method to estimate covariance matrix, introduced by Lediot and Wolf in this paper [2]
For SAAM algorithm, the following two parameters are available.
Returns Moments Estimator & Returns Resampling Model
These parameters are only for SAAM Algorithm. We now only provide Ledoit Wolf 2002 as returns moments estimator (this link) [3] and block bootstrap as returns resampling model.
Risk Aversion Coefficient
This is the λ in the model like Markowitz’s, like
\(\max \limits_w w^Tr-\lambda w^T\Sigma w\)
s.t. \(w^T1=1\)
Besides, we provide several constraint options for SOCP, Markowitz & SAAM.
*For Markowitz, its quadratic programming only enables you to configure Position Limits.
Constraints (Optional)
―Market Impact:
Market impact describes the impact of investments to the market, which means, your investment weight vector w can influence expected return vector r.
We use non-linear model to depict this relationship, which is \(r_i^{′}=r_i-l_i \sqrt{w_i }\), where \(l_i\)s are square root impact coefficients. Larger it is, larger impact the corresponding asset has on the market.
To set square root impact coefficient for an asset,
tick the check box of the asset, fill in the number you want to set in the input box below, and click “Update”.
If you want to set the same coefficient for every asset, tick the check box 
on the top left corner to select all, fill in the number in the box below and click “Update”.
You can set other constraints in the same way as the introduction in the last slide.
―Position Limits:
Allowed minimum and maximum weight for any given assets.
e.g. If you set minimum weight as 0, then short selling will not beallowed.
―Black List:
Weights of black-listed assets will not be changed during transactions.
―Max Loan:
This decides the minimal allowed weight of asset during transactions.
e.g. If you set max loan as 0.3, then the weight of asset can be at least -0.3.
Adding New Model
First, select a portfolio optimization algorithm.
If your algorithm is not 1/N,
then, choose the estimation models and click “add”;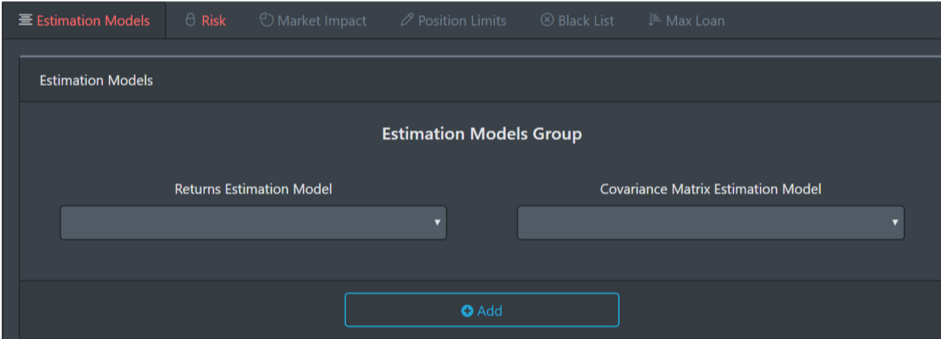
Then, click Risk tab and set risk aversion coefficient and constraints (introduced in former slides) .
Finally click “Finish the SOCP configuration”. 
After finishing adding new models, click “Next” to configure diversification method.
5. Diversification
If you have chosen Markowitz, SOCP or SAAM method before, you will be able to choose whether to use Corvalan algorithm to do some diversification.
Corvalan Algorithm
Corvalan method adds a tolerance term in strict equalities of the original model.
Suppose the optimal solution of the original problem is w, the corresponding expected return is \(R=w^Tr\), and variance is \(\sigma=w^T\Sigma w\). Then Corvalan method solves the model below:
\(\min\limits_{v}f(v)\)
s.t. \(v^Tr\geq R(1-\Delta r)\), \(v^T\Sigma_v\leq\sigma (1-\Delta\sigma)\) and other constraints
where f(v) is a function that will be very large if v fails to be well-diversified.
This algorithm solves the problem that the weight vector calculated by Markowitz-like models often concentrate on only several assets.
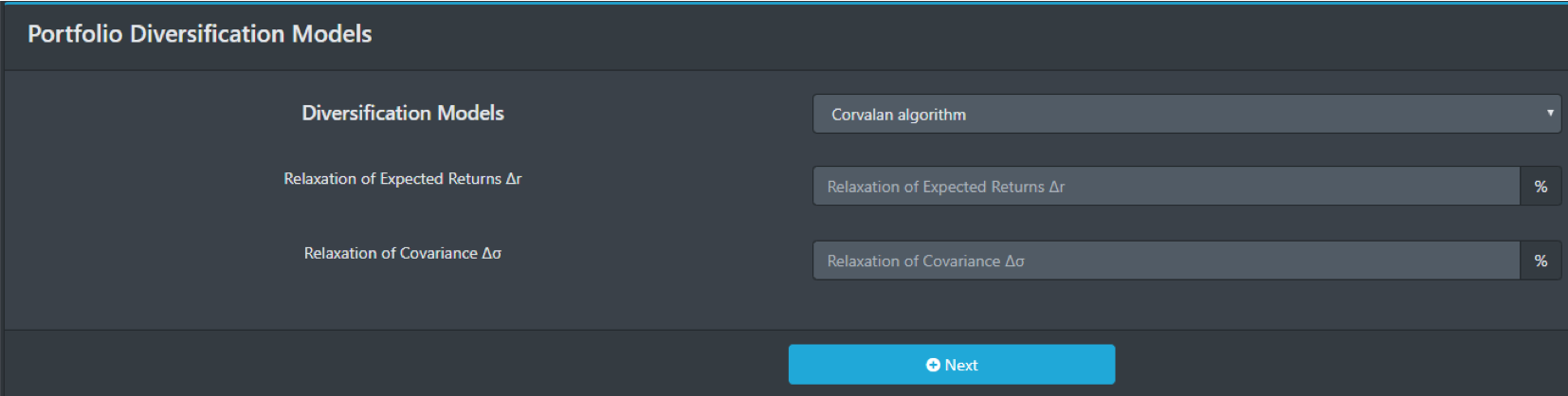
To add diversification model, just select Corvalan algorithm and set Relaxation of Expected Returns
Δr(%) and Relaxation of Covariance Δσ(%) and click “Next”. They are parameters in the model below:
\(\min\limits_{v}f(v)\)
s.t. \(v^Tr\geq R(1-\Delta r)\), \(v^T\Sigma_v\leq\sigma (1-\Delta\sigma)\) and other constraints
6. Run & Check
After configuring models, we go to the page “configurations of models”.
Tick the configurations you would like to simulate and click “Run the Selected Configurations”.
After simulations accomplish, the system would send you a prompt.
Click “Reports” on the left to check the results. 
In this page, you can either check the results separately, or check them together and compare.
If you just want to check one result, click its Configuration Name.
Reports include profit & loss plot, vital performance measures, weight over time and executions.
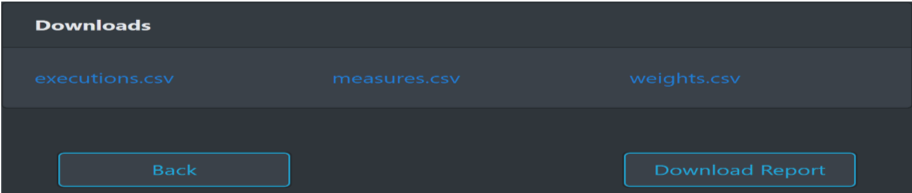
You can download report including details.
We also provide .csv format file (executions, measures, weights) for you to download and analyze.
To compare several models, tick them all and click “Simulation Comparison”.
The system will plot their profit & loss on the same canvas, and provide the comparison of vital performance measures.
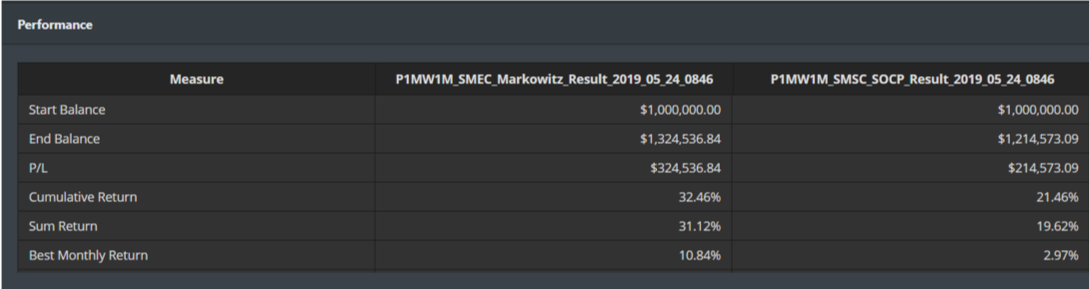
Performance Measures
We provide 32 measures on the webpage to help you to analyze whether your model performances well.
For example
―Cumulative Return;
―Commission;
―Max. Drawdown%:
The worst (the maximum) peak to valley loss since the investment’s inception.
―Execution Count:
The number of sell/buy orders you have made.
―Treynor ratio:
The risk premium obtained per unit of risk. The greater the Treynor index, the higher the unit risk premium is and the better the performance of the portfolio is. Calculation follows below:
\(TR=\frac{R_p-R_f}{\beta_p}\)
These measures could all be found in measures.csv . You can download it and see more detailed analysis.
Notice selected stocks will be automatically propagate to the portfolios of following rebalancing dates, which means the portfolio will not change in the following rebalancing dates even if some of the stocks are not fit the filters.Step 2: Add portfolio-optimization algorithms